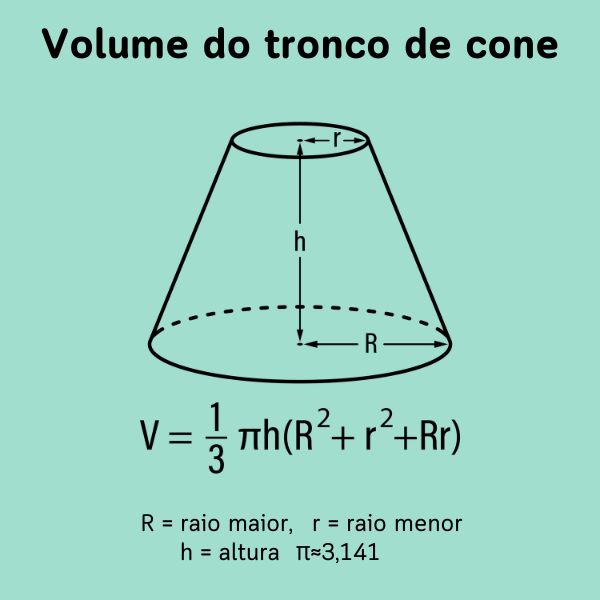
O volume do tronco de cone é o espaço ocupado por esse sólido ou a sua capacidade de armazenamento. Quando um cone é seccionado por um plano, ele é decomposto em dois sólidos: um cone menor e um tronco de cone. Assim, o volume de um tronco de cone é a diferença entre o cone original e o cone menor, decomposto do primeiro após a secção.
Para calcular o volume do tronco de cone, é necessário conhecer as medidas dos raios de suas bases circulares e a sua altura.
Leia também: Como calcular área e volume do tronco da pirâmide
Tópicos deste artigo
- 1 - Resumo sobre volume do tronco de cone
- 2 - Videoaula sobre o volume do tronco de cone
- 3 - Elementos do tronco de cone
- 4 - Qual a fórmula do volume do tronco de cone?
- 5 - Como se calcular o volume do tronco de cone?
- 6 - Exercícios resolvidos sobre o volume do tronco do cone
Resumo sobre volume do tronco de cone
- O volume do tronco de cone refere-se ao espaço que ele ocupa.
- Para determinar esse volume, são necessários os raios de suas bases e sua altura.
- A fórmula do volume do tronco de cone é: \(V=\frac{1}{3}\pi h(R^2+Rr+r^2)\).
Videoaula sobre o volume do tronco de cone
Elementos do tronco de cone
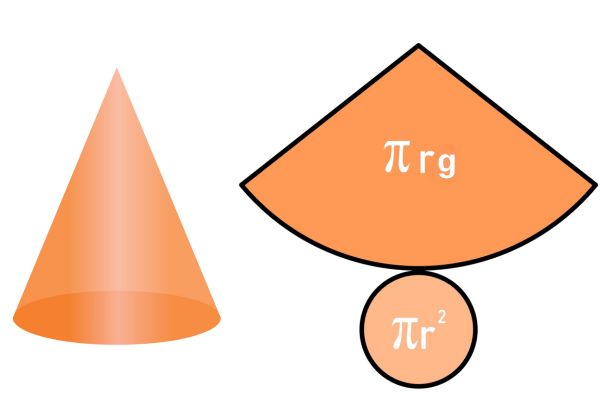
O tronco de cone se origina da secção entre um cone e um plano (paralelo ou não à sua base). Por esse corte, o cone pode ser decomposto em outras duas figuras espaciais, uma delas é um cone menor que o original e a outra é o tronco de cone, um sólido composto de duas bases circulares não congruentes.

Por conta dessa decomposição, os principais elementos do tronco de cone são relacionados à sua altura e às medidas dos círculos que compõem suas bases:
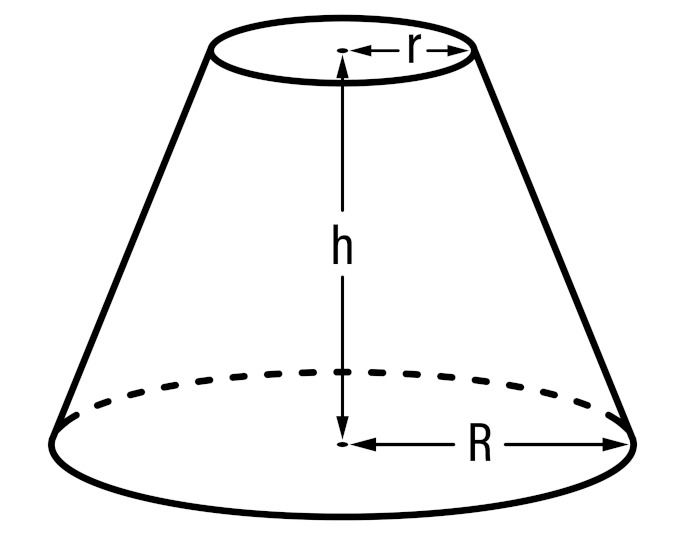
- Raio da base menor (r): é a medida do raio do círculo da base menor.
- Raio da base maior (R): é a medida do raio do círculo da base maior.
- Altura (h): é a distância vertical entre a base menor e a base maior do tronco de cone.
Qual a fórmula do volume do tronco de cone?
Para determinar a fórmula do volume do tronco de cone, deve-se analisar a decomposição do cone que o origina:
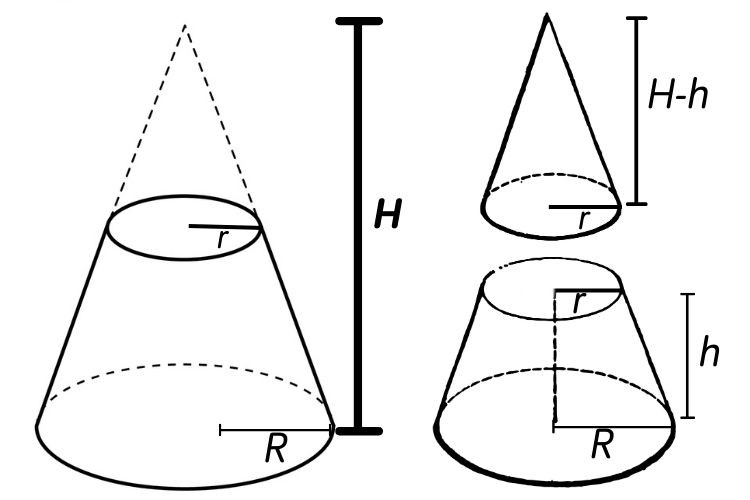
Assim, para calcular o volume do tronco do cone, basta calcular o volume do cone maior que o originou e subtrair desse valor o volume do cone menor que aparece na decomposição do sólido.
Assim, o volume do tronco de cone é dado pela relação:
|
Volume do tronco de cone=Volume do cone maior-Volume do cone menor |
Sabendo que o volume de um cone é dado por:
\(V=\frac{1}{3}\pi R^2H\ \)
O volume do tronco de cone é dado por:
\(V_T=\frac{1}{3}\pi R^2H-\frac{1}{3}\pi r^2(H-h)\)
\(V_T=\frac{1}{3}\pi\left[R^2H-r^2(H-h)\right]\)
\(V_T=\frac{1}{3}\pi\left(R^2H-r^2H+r^2h\right)\)
\(V_T=\frac{1}{3}\pi\left[(R^2-r^2)\ H+r^2h\right]\)
Agora, para finalizar a dedução da fórmula, relaciona-se a altura H do cone com as medidas do tronco de cone, de modo a substituí-la na fórmula. Para isso, observe determinada parte da secção meridiana do cone original:
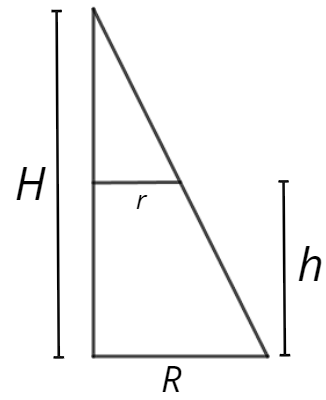
Nesse caso, é possível relacionar proporcionalmente as medidas que aparecem nessa secção do seguinte modo:
\(\frac{r}{R}=\frac{H-h}{H}\)
\(R(H-h)=rH\)
\(RH-Rh=rH\)
\(RH-rH=Rh\)
\((R-r)H=Rh\)
\(H=\frac{Rh}{R-r}\)
Assim, substituindo essa relação na fórmula, no lugar de H:
\(V_T=\frac{1}{3}\pi\left[(R^2-r^2)\frac{Rh}{R-r}+r^2h\right]\)
Expandindo a fatoração \(R^2-r^2=(R+r)(R-r)\), tem-se:
\(V_T=\frac{1}{3}\pi\left[(R+r)(R-r)\frac{Rh}{R-r}+r^2h\right]\)
\(V_T=\frac{1}{3}\pi\left[\left(R+r\right)Rh+r^2h\right]\)
\(V_T=\frac{1}{3}\pi\left[R^2h+Rrh\ +r^2h\right]\)
\(V_T=\frac{1}{3}\pi h\left[R^2+Rr\ +r^2\right]\)
Assim, se h é a altura do tronco de cone, R é o raio do círculo da base maior e r é o raio do círculo da base menor, o volume do tronco de cone é dado por:
\(V_T=\frac{1}{3}\pi h(R^2+Rr\ +r^2)\)
Como se calcular o volume do tronco de cone?
É possível calcular o volume do tronco de cone sabendo a medida dos raios de seus dois círculos e a sua altura, como mostra o exemplo a seguir.
- Exemplo 1: Calcule o volume de um tronco de cone cuja altura mede 10 cm, o raio da base maior mede 6 cm e o raio da base menor mede 5 cm. (Use π=3)
Com as informações dadas e utilizando a fórmula do volume do tronco de cone, calcula-se:
\(V_T=\frac{1}{3}\pi h(R^2+Rr\ +r^2)\)
\(V_T=\frac{1}{3}\cdot3\cdot10\cdot(6^2+6\cdot5\ +5^2)\)
\(V_T=10\cdot(36+30\ +25)\)
\(V_T=10\cdot\left(91\right)=910\ cm^3\)
Leia também: Como calcular área e volume do cubo
Exercícios resolvidos sobre o volume do tronco do cone
Questão 1
(Mackenzie) Uma xícara de chá tem a forma de um tronco de cone reto, conforme a figura.
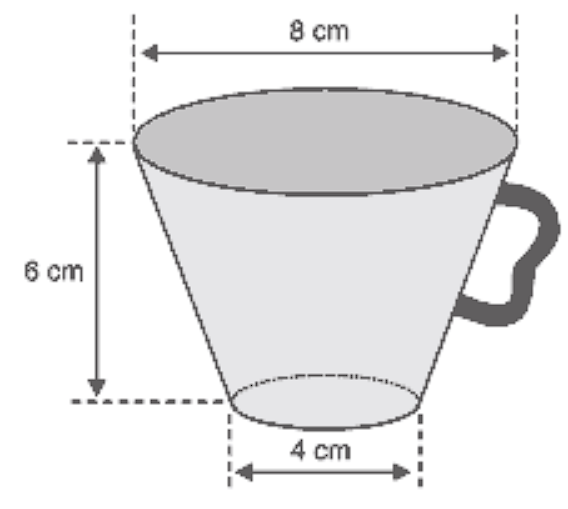
Supondo π=3 , o volume máximo de líquido que ela pode conter é:
a) 168 cm3
b) 172 cm3
c) 166 cm3
d) 176 cm3
e) 164 cm3
Gabarito: letra a)
Resolução:
Para resolver essa questão, deve-se utilizar os dados apresentados na figura para calcular o volume da xícara.
Para isso, deve-se perceber que a imagem fornece os diâmetros das bases, de modo que seus raios consistem na metade dessas medidas, ou seja:
\(raio\ da\ base\ menor=\frac{4\ cm}{2}=2\ cm\)
\(raio\ da\ base\ maior=\frac{8\ cm}{2}=4\ cm\)
Tomando \(r=2,\ R=4,\ h=6\) e utilizando π=3, tem-se:
\(V_T=\frac{1}{3}\pi h(R^2+Rr\ +r^2)\)
\(V_T=\frac{1}{3}\cdot3\cdot6\cdot(4^2+4\cdot2\ +2^2)\)
\(V_T=6\cdot(16+8\ +4)\)
\(V_T=6\cdot\left(28\right)=168\ cm^3\)
Logo, a alternativa correta é a alternativa a).
Questão 2
(Mackenzie) A figura representa o sorvete “choconilha”, cuja embalagem tem a forma de um cone circular reto. O cone é preenchido com sorvete de chocolate até a altura de 12 cm e, o restante, com sorvete de baunilha.
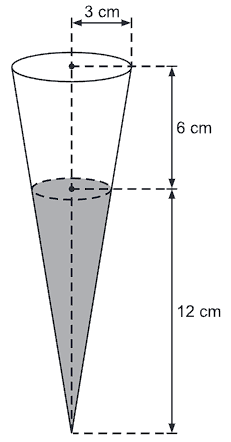
Adotando π=3, o número máximo de sorvetes que é possível embalar, com 2 litros de sorvete de baunilha e 1 litro de sorvete de chocolate, é:
a) 21
b) 22
c) 18
d) 17
e) 19
Gabarito: d)
Resolução:
Para resolver essa questão, primeiramente deve-se determinar a medida do raio do círculo da base menor do tronco de cone. Para isso, deve-se atentar à seguinte proporção:
\(\frac{r}{3}=\frac{12}{12+6}\)
\(\frac{r}{3}=\frac{12}{18}\)
\(18r=12\cdot3\)
\(r=\frac{36}{18}=2\ cm\)
Com base nessa medida, deve-se calcular o volume de chocolate e o volume de baunilha que são colocados em um sorvete.
Para calcular o volume de chocolate, utiliza-se a fórmula do volume do cone:
\(volume\ chocolate=\frac{1}{3}\pi r^2h\)
\(volume\ chocolate=\frac{1}{3}\cdot3\cdot2^2\cdot12\)
\(volume\ chocolate=4\cdot12=48\ cm^3\)
Para calcular o volume de baunilha, utiliza-se a fórmula de volume do tronco de cone:
\(volume\ baunilha=\frac{1}{3}\pi h(R^2+Rr\ +r^2)\)
\(volume\ baunilha=\frac{1}{3}\cdot3\cdot6(3^2+3\cdot2\ +2^2)\)
\(volume\ baunilha=6\left(9+6\ +4\right)=6\cdot19=114\ cm^3\)
Agora, sabendo que um 1 litro equivale a 1000 cm3, o máximo de sorvetes que ele consegue embalar com 1 litro de sorvete de chocolate e com 2 litros de sorvete de baunilha é:
\(n° de \ sorvetes\ de \ chocolate= \frac{1\ litro}{48 cm^3}=\frac{1000 cm^3}{48 cm^3}≅20,8=20 sorvetes\)
\(n° de \ sorvetes\ de \ baunilha= \frac{2litros}{114 cm^3}=\frac{2000 cm^3}{114 cm^3}≅17,5=17 sorvetes\)
Portanto, como cada sorvete inteiro tem uma parte de chocolate e uma de baunilha, o máximo de sorvetes completos que ele consegue fazer é 17 .
A alternativa correta é a alternativa d).
Fontes:
ALMEIDA, Célio Pinto de. Geometria espacial. 1. ed. Rio de Janeiro: G. Ermakoff, 2018.
DOLCE, Osvaldo; NICOLAU, José. Fundamentos de matemática elementar 10 – Geometria espacial. 5. ed. Santos: Atual, 1993.