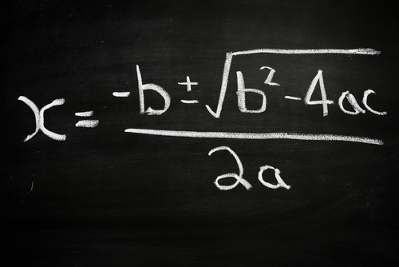No estudo de álgebra, lidamos muito com equações, tanto do 1° quanto do 2° grau. Em geral, uma equação do 2° grau pode ser escrita da seguinte forma:
ax2 + bx + c = 0
Os coeficientes da equação do 2° grau são a, b e c. Essa equação recebe esse nome porque a incógnita x está elevada à segunda potência ou ao quadrado. Para resolvê-la, o método mais comum é a utilização da Fórmula de Bhaskara. Esta garante que o resultado de qualquer equação do 2° grau pode ser obtido através da fórmula:
x = – b ± √? , onde ? = b2 – 4.a.c
2.a
Através dessa fórmula, obtemos duas raízes, uma delas é obtida utilizando o sinal positivo antes da raiz quadrada de delta e outra utilizando o sinal negativo. Podemos então representar as raízes da equação do 2° grau como x1 e x2 da seguinte forma:
x1 = – b + √?
2.a
x2 = – b – √?
2.a
Vamos tentar estabelecer relações entre a soma e produto dessas raízes. A primeira delas pode ser obtida pela soma. Teremos, então:
x1 + x2 = – b + √? + (– b – √?)
2.a 2.a
x1 + x2 = – b + √? – b – √?
2.a
Como as raízes quadradas de delta possuem sinais opostos, elas anular-se-ão, restando apenas:
x1 + x2 = – 2.b
2.a
Simplificando a fração resultante por dois:
x1 + x2 = – b
a
Portanto, para qualquer equação do 2° grau, se somarmos suas raízes, obteremos a razão – b/a. Vejamos uma segunda relação que pode ser obtida pela multiplicação das raízes x1 e x2:
x1 . x2 = – b + √? . – b – √?
2.a 2.a
x1 . x2 = (– b + √?).(– b – √?)
4.a2
Aplicando a propriedade distributiva para fazer a multiplicação entre os parênteses, obtemos:
x1 . x2 = b2 + b.√? – b.√? -- (√?)2
4.a2
Como os termos b.√? possuem sinais opostos, eles anulam-se. Também calculando (√?)2 , temos que (√?)2 = √?.√? = ?. Lembrando ainda que ? = b2 – 4.a.c. Portanto:
x1 . x2 = b2 – ?
4.a2
x1 . x2 = b2 – (b2 – 4.a.c)
4.a2
x1 . x2 = b2 – b2 + 4.a.c
4.a2
x1 . x2 = 4.a.c
4.a2
Considerando que a2 = a.a, podemos simplificar a fração, dividindo o numerador e o denominador por 4.a, obtendo:
x1 . x2 = c
a
Essa é a segunda relação que podemos estabelecer entre as raízes de uma equação do 2° grau. Ao multiplicar as raízes, encontramos a razão c/a. Essas relações de soma e produto das raízes podem ser empregadas mesmo que estejamos trabalhando com uma equação do 2° grau incompleta.
Agora que conhecemos as relações que podem ser obtidas através da soma e produto das raízes de uma equação do 2° grau, vamos resolver dois exemplos:
-
Sem resolver a equação x2 + 5x + 6 = 0, determine:
a) A soma de suas raízes:
x1 + x2 = – b
a
x1 + x2 = – 5
1
x1 + x2 = – 5
b) O produto de suas raízes:
x1 . x2 = c
a
x1 . x2 = 6
1
x1 . x2 = 6
-
Determine o valos de k para que a equação tenha duas raízes x2 + (k – 1).x – 2 = 0, cuja soma seja igual a – 1.
A soma de suas raízes é dada pela seguinte razão:
x1 + x2 = – b
a
x1 + x2 = – (k – 1)
1
Mas nós temos definido que a soma das raízes é – 1
– 1 = – (k – 1)
1
– k + 1 = – 1
– k = – 1 – 1
(--1). – k = – 2 .(--1)
?k = 2
Portanto, para que a soma das raízes dessa equação seja – 1, o valor de k deve ser 2.