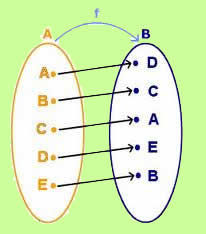
Na Matemática, consideramos função como uma relação de dependência entre duas grandezas. As relações que envolvem crescimentos e decrescimentos lineares são representadas por uma função do 1º grau do tipo y = ax + b, com a e b números reais e b ≠ 0. Nessa função, os pares ordenados (x, y) são denominados domínio e imagem respectivamente. A representação desse modelo de função no plano cartesiano é dada por uma reta crescente ou decrescente. A posição da reta no plano depende do valor do coeficiente angular a, caso ele seja positivo (a > 0), a reta é crescente; e se for negativo (a < 0), a reta é decrescente. O coeficiente representado por b é denominado linear e indica em que ponto do eixo y (ordenada) a reta passa.
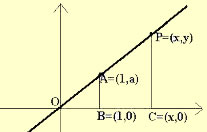
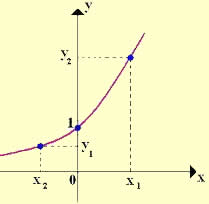
O gráfico da função é construído no plano de coordenadas cartesianas, onde cada valor de x (eixo das abscissas) possui uma representação em y (eixo das ordenadas).
.jpg)
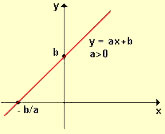
Função do 1º grau crescente – (a > 0)
A função y = 2x + 5 é representada por uma reta crescente, pois o coeficiente angular é positivo, possuindo valor igual a 2. Veja o gráfico:
.jpg)
Na função crescente, à medida que os valores de x aumentam, os valores de y também aumentam; ou à medida que os valores de x diminuem, os valores de y diminuem.
Função do 1º grau decrescente – (a < 0)
A função y = –2x +3 é representada por uma reta decrescente, pois o coeficiente angular é negativo, possuindo valor igual a –2. Veja o gráfico:
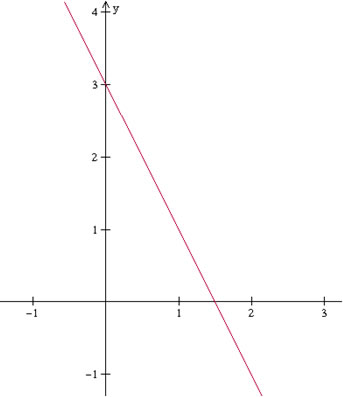
Na função decrescente, à medida que os valores de x aumentam, os valores de y diminuem; ou, à medida que os valores de x diminuem, os valores de y aumentam.
Aproveite para conferir nossa videoaula relacionada ao assunto: