Uma função é uma regra que liga cada elemento de um conjunto A a um único elemento de um conjunto B. No Ensino Fundamental, as funções estudadas possuem apenas duas variáveis.
A primeira é chamada de variável independente, é geralmente representada pela letra x e pode assumir qualquer valor dentro de um conjunto numérico dado. A segunda, chamada de variável dependente, costuma ser representada pela letra y e seu valor está relacionado com o valor da variável x. A função do segundo grau é uma regra que possui as características descritas acima e, pelo menos, uma variável independente elevada ao quadrado.
As funções do segundo grau, portanto, relacionam a variável x à variável y e são escritas, geralmente, na forma reduzida a seguir:
f(x) = y = ax2 + bx + c
-
a, b e c são números reais quaisquer;
-
a sempre é diferente de zero;
-
f(x) é uma segunda notação muito utilizada nesse conteúdo que ajuda na organização dos cálculos.
Exemplos de função do segundo grau
Os exemplos a seguir são de funções do segundo grau:
a) y = 2x2 + 2x + 3. Observe que a = 2, b = 2 e c = 3;
b) y = 3x2 – 9. Observe que a = 3, b = 0 e c = – 9;
c) f(x) = x2. Observe que a = 1, b = 0 e c = 0;
Domínio e imagem
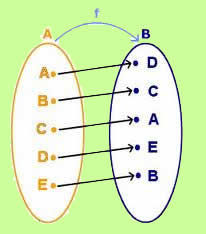
As funções do segundo grau, assim como qualquer função, possuem domínio, contradomínio e imagem. Tendo em vista a definição dada no início do texto:
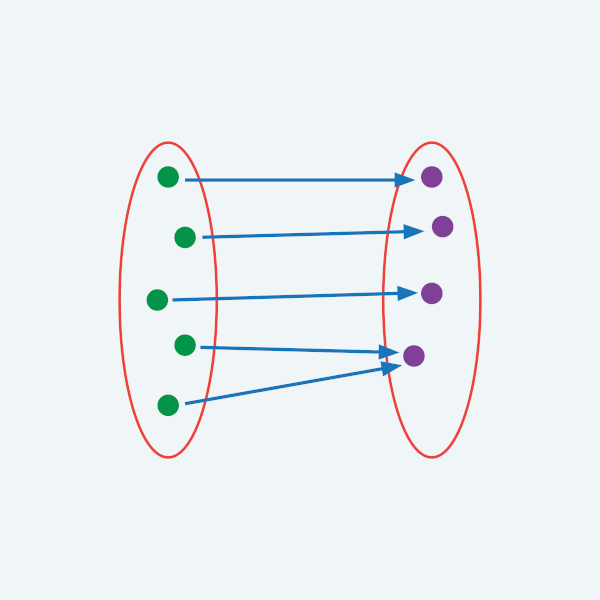
“Uma função é uma regra que liga cada elemento de um conjunto A a um único elemento de um conjunto B.”
A variável independente x pode assumir qualquer valor entre os elementos do conjunto A. Como ela “comanda” o resultado encontrado na variável y, então o conjunto A é “dominante” e é chamado de Domínio. Por sua vez, a variável independente pode assumir qualquer valor entre os elementos do conjunto B; assim, esse conjunto recebe o nome de Contradomínio.
É obrigatório que a função faça “ligações entre conjuntos” usando todos os elementos do conjunto A, mas nem sempre todos os elementos do conjunto B. Todos os elementos do conjunto B que são imagem de algum elemento do conjunto A são chamados de Imagem.
Na função do segundo grau f(x) = y = x2, por exemplo, cujo domínio e o contradomínio são o conjunto dos números reais, temos os seguintes resultados:
x = 3, então y = 32 = 9;
x = 2, então y = 22 = 4;
x = 1, então y = 12 = 1;
x = – 1, então y = (– 1)2 = 1;
x = – 2, então y = (– 2)2 = 4.
Observe que, para valores positivos de x, a função apresenta imagens positivas e, para valores negativos de x, a função também apresenta imagens positivas. Como a função foi definida com contradomínio nos números reais, os números negativos não são resultados possíveis e a imagem fica sendo apenas o conjunto dos números reais não negativos.
Raízes da função do segundo grau
As raízes de uma função são os valores que a variável independente assume e que fazem com que a imagem da função seja zero. Assim, para encontrar as raízes de uma função do segundo grau, escreva y = 0 e substitua y por esse valor. Observe o exemplo:
y = x2 + 8x – 9
0 = x2 + 8x – 9
Dessa maneira, encontraremos os valores de x que zeram a função. Para tanto, utilizaremos a fórmula de Bhaskara ou o método de completar quadrados.
x2 + 8x – 9 = 0
x2 + 8x = 9
x2 + 8x + 16 = 9 + 16
x2 + 8x + 16 = 25
(x + 4)2 = 25
√[(x + 4)2] = √25
x + 4 = ± 5
x = – 4 ± 5
x' = – 4 – 5
x' = – 9
x'' = – 4 + 5
x'' = 1
Assim, as raízes dessa função são – 9 e 1.
O gráfico de uma função do segundo grau
Toda função pode ser representada por um gráfico em um plano cartesiano. A figura relacionada com a função do segundo grau é a parábola. Essa figura pode ser obtida marcando-se ponto a ponto de um plano cartesiano os resultados obtidos ao procurar valores de y relacionados com cada valor de x. Se desenharmos todos os pontos da função y = x2, visualizaremos o seguinte gráfico:
.jpg)
Esse gráfico pode ser desenhado de maneira prática com apenas três de seus pontos – vértice e raízes ou vértice e dois pontos aleatórios em que um está à direita e outro está à esquerda do vértice.
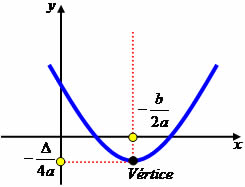
O vértice é o ponto mais alto ou o ponto mais baixo de uma parábola. No caso do exemplo acima, é o ponto mais alto o que toca o ponto (0,0). Para encontrar suas coordenadas (xv, yv) podemos utilizar as seguintes fórmulas:
xv = – b
2a
yv = –Δ
4a
*Δ = b2 – 4ac.
Para encontrar as raízes e desenhar a parábola, utilize a fórmula de Bhaskara ou qualquer método conhecido. Caso não haja raízes ou por qualquer outro motivo não exista a possibilidade desse cálculo, faça o seguinte:
1 – Encontre as coordenadas do vértice;
2 – Faça xv + 1 e calcule o valor de y correspondente a esse número;
3 – Faça xv – 1 e calcule o valor de y correspondente a esse número.
Os quatro valores obtidos acima serão as coordenadas dos pontos que podem ser usados para desenhar a parábola.
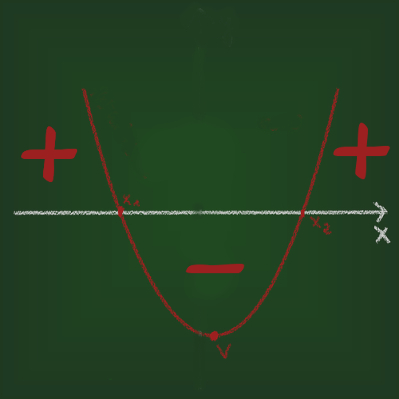
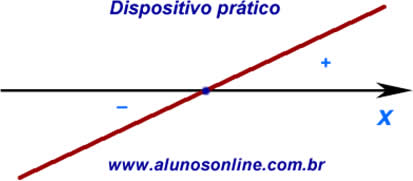
Análise do sinal
Tendo em vista que a função do segundo grau é uma parábola, é possível analisar o sinal de Δ para saber quantas raízes essa função terá. A raiz de uma função é o valor de x que faz y igual a zero. Dessa maneira, no gráfico, uma raiz é o ponto em que a parábola encontra-se com o eixo x.
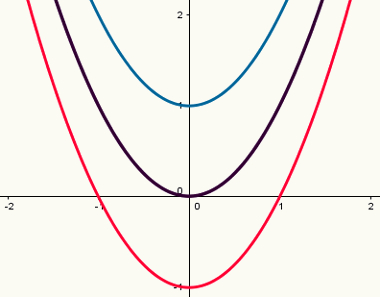
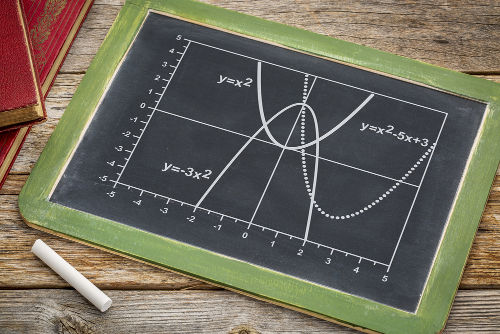
Três funções parecidas que possuem número diferente de raízes
As parábolas na imagem acima representam funções do segundo grau e possuem um número diferente de raízes. A primeira, em azul, é o gráfico da função y = x2 + 1, que não possui raízes reais. Observe que o valor de Δ dessa função é negativo e é justamente por esse motivo que concluímos a não existência de raízes reais.
A segunda função, em roxo, é o gráfico de y = x2. Observe que existe apenas uma raiz real, x = 0 e Δ = 0.
A terceira função, em vermelho, é gráfico de y = x2 – 1. Observe que ela possui duas raízes reais, x = 1 e x = – 1, e que Δ é maior que zero.
Concluímos, então, que, quando uma função possui Δ < 0, ela não possui raízes reais. Quando uma função possui Δ = 0, existe apenas uma raiz real e, quando Δ > 0, a função possui duas raízes reais distintas.
Ponto de máximo e mínimo
O ponto de máximo e o ponto de mínimo coincidem com o vértice de uma parábola e são, respectivamente, o ponto mais alto e o ponto mais baixo que uma parábola pode atingir.
Se uma parábola possui o vértice voltado para baixo, então ela possui um ponto de mínimo e não possui ponto de máximo, pois segue infinitamente para cima, e vice-versa.
Não é necessário construir o gráfico de uma função sempre que for pedido seu ponto de máximo ou mínimo. Para encontrar as coordenadas desses pontos, basta encontrar as coordenadas do vértice (xv, yv). Entenda como fazer isso com os macetes a seguir:
Macetes
Existem alguns macetes para funções do segundo grau parecidos com a análise dos sinais acima.
Quando a > 0, o gráfico da função é uma parábola com a “boca” voltada para cima e o vértice para baixo (o vértice é ponto de mínimo);
Quando a < 0, o gráfico da função é uma parábola com a “boca” voltada para baixo e o vértice para cima (o vértice é ponto de máximo);
O valor de c indica o ponto de intersecção da parábola com o eixo y.
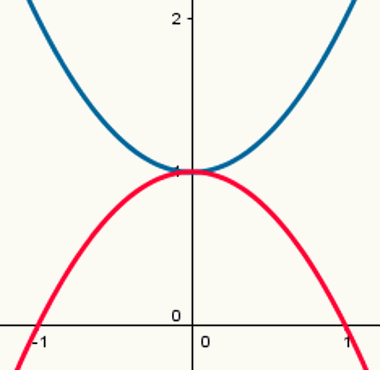
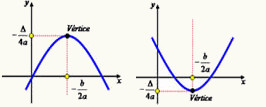
Duas funções: uma com ponto de máximo e outra com ponto de mínimo
Observe que a parábola azul possui ponto de mínimo e a parábola vermelha possui ponto de máximo. Suas leis de formação são, respectivamente:
y = x2 + 1
y = – x2 +1
Seus respectivos valores de a são 1 e – 1.
Aproveite para conferir nossas videoaulas sobre o assunto: