A classificação de polígonos pode ser feita quanto ao seu número de lados ou ângulos, que é o que nomeia os polígonos como regulares ou irregulares. O polígono é regular se possuir todos os lados congruentes, ou seja, com a mesma medida, e irregular caso contrário. Outra classificação de polígonos importante é a de convexo e não convexo: o polígono é convexo se todos os seus ângulos internos forem menores que 180º e não convexo caso contrário.
Leia também: Como calcular a área dos polígonos
Tópicos deste artigo
Como classificar os polígonos?
-
Classificação dos polígonos quanto ao número de lados
A classificação do polígono quanto ao número de lados é de grande importância, pois é a partir do número de lados de um polígono que podemos nomeá-lo. O número de lados e o número de ângulos internos de um polígono são sempre iguais. Por exemplo, o triângulo é assim chamado porque “tri” faz menção a três, ou seja, três ângulos. O polígono de quatro lados é conhecido como quadrilátero, e posteriormente os polígonos são igualmente nomeados com prefixo que demonstra quantidade, como penta, hexa, hepta e assim sucessivamente, seguido do sufixo -gono, que significa ângulo.
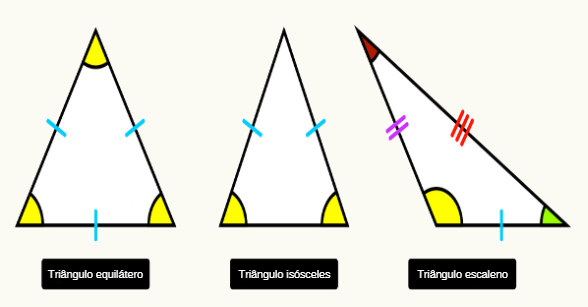
Triângulo – três lados
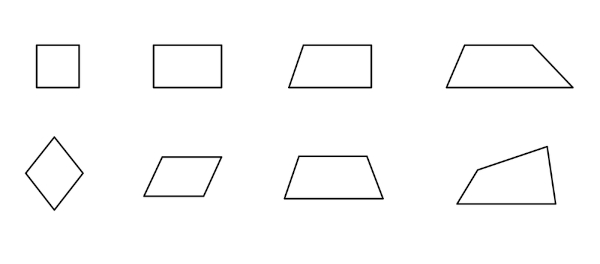
Quadrilátero – quatro lados
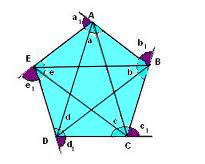
Pentágono – cinco lados
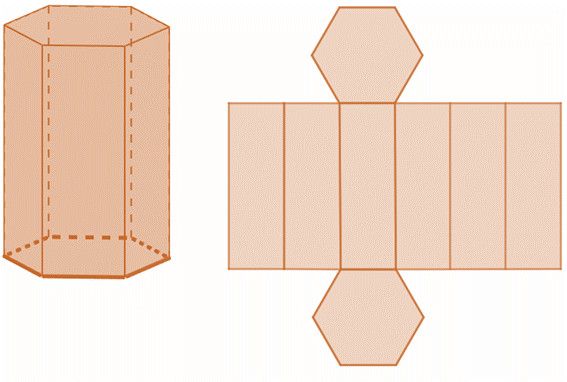
Hexágono – seis lados
Heptágono – sete lados
Octógono – oito lados
Eneágono – nove lados
Decágono – dez lados
-
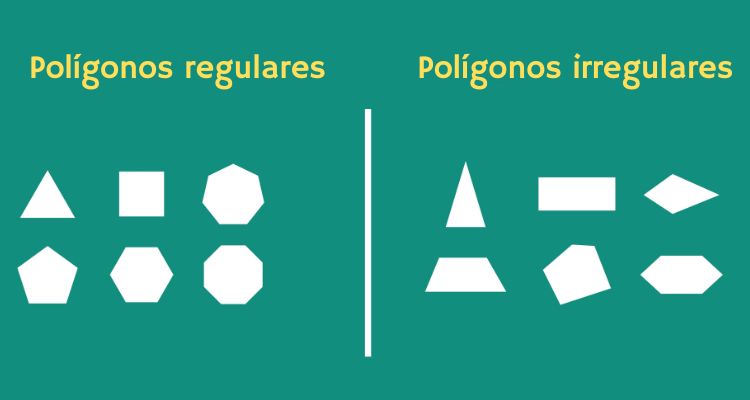
Polígono regular e irregular
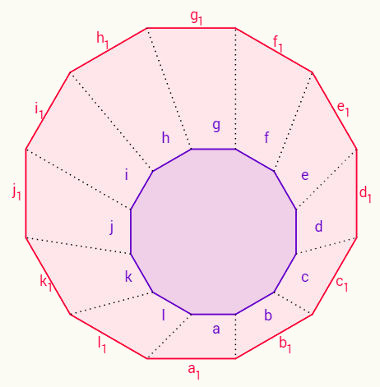
O polígono pode ser classificado como regular ou irregular. Ele é considerado regular se os seus lados possuem as mesmas medidas e os seus ângulos também possuem a mesma medida, ou seja, é um polígono equilátero e equiângulo. Caso contrário, o polígono é conhecido como irregular.
-
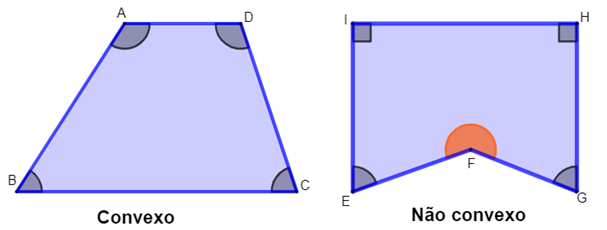
Polígonos convexos e não convexos
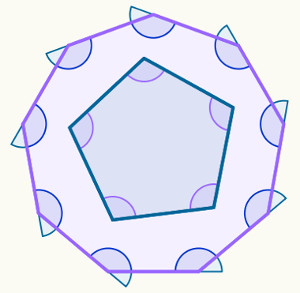
O polígono pode ser convexo ou não convexo. O não convexo é conhecido também como côncavo. Existem diferentes formas de diferenciar o polígono como convexo ou não convexo, uma dessas maneiras é levando em consideração a medida dos seus ângulos internos. O polígono é convexo se seus ângulos internos forem todos menores que 180º e não convexo caso ele tenha um ângulo interno maior que 180º.
Exercícios resolvidos sobre classificação dos polígonos
Questão 1
Sabemos que os polígonos podem ser classificados como convexos e não convexos e como regulares ou irregulares. De acordo com essas possíveis classificações, julgue as afirmativas a seguir:
I – Todo polígono convexo é também regular.
II – O retângulo e o trapézio são quadriláteros.
III – Todo polígono que possui lados congruentes é um polígono regular.
Marque a alternativa correta:
A) Somente a I é verdadeira
B) Somente a II é verdadeira
C) Somente a III é verdadeira
D) Todas são falsas.
Resolução:
Alternativa B
I – Todo polígono convexo é também regular. (falsa)
O polígono pode ser convexo e não possuir lados e ângulos congruentes, ou seja, ser convexo e irregular.
II – O retângulo e o trapézio são quadriláteros. (verdadeira)
III – Todo polígono que possui lados congruentes é um polígono regular. (falsa)
Os lados congruentes não são o suficiente para classificar como regular, pois é necessário que os ângulos também sejam congruentes.
Questão 2
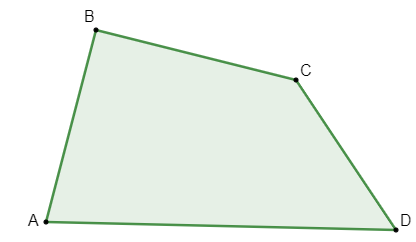
Sabemos que os polígonos são classificados quanto ao número de lados e à sua forma. Analisando o polígono a seguir, ele pode ser classificado como:
A) Quadrilátero, regular e convexo
B) Quadrilátero, irregular e convexo
C) Quadrilátero, irregular e não convexo
D) Pentágono, regular e convexo
E) Pentágono, regular e não convexo
Resolução:
Alternativa B
Note que ele possui 4 lados, logo ele é um quadrilátero. Além disso, esses lados não são congruentes, sendo assim ele é um quadrilátero irregular. Por fim, ele não possui nenhum ângulo maior que 180°, sendo assim esse polígono é um quadrilátero irregular convexo.
Fontes:
DANTE, Luiz Roberto. Matemática: contexto e aplicações. Volume 3. 3. ed. São Paulo: Ática, 2011.
GIOVANNI, José Ruy; CASTRUCCI, Benedito; GIOVANNI JR, José Ruy. A Conquista da Matemática. Volume 3. 10. ed. São Paulo: FTD, 2014.